ROLF MICHAEL

摘要：
以板型几何形状铸件为例，研究第一浇铸阶段，活塞速度对压室充填过程的影响。通过数字计算，可识别优化运行速度。借助于自动优化所确定的堵塞波值与同活塞同步的堵塞度波是一致的。对浇铸构件实验检查，证实了此理论研究。
一、 前言
压铸第1阶段，慢压射起始速度V1，除了影响充填度，容室长度及直径，还影响金属熔化物流动。对构件的浇铸质量有一定影响。过高的活塞起始速度会导致容室内金属熔化物的涡流，从而对气体喷冲（见图1），如果速度选得过低，会形成推进冲击波，在早期阶段就会对浇道堵塞。在容室内的空气不能排出，与金属熔化物压缩在一起。在此两种情况下会导致构件内气体孔隙度增加。由于在容室壁上熔化物的快速冷却以及与此相关的预冷凝，十分低的起始速度是错误的。
 

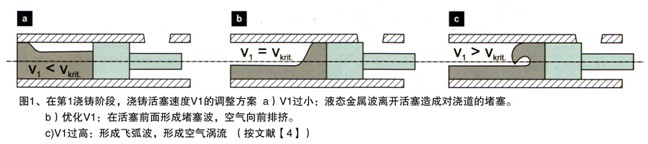
作为理想的情况，根据相关文献对第1阶段的起始速度作的论述，该速度下在活塞前边产生一个堵塞波，不离开活塞面，由此，在浇铸容室内空气向前进入浇道，防止形成飞弧及空气喷冲，这样的速度称之为临界速度，与容室的几何形状（直径和长度）及充填度有关。这样的速度可以一个固定的起始速度，也可以通过活塞稳定加速度来说明。
通过数字计算，对浇铸容室内充填过程的研究不难理解，由于多种原因，例如高的温度或有限的空间通道，只进行实验观察是难以转化的，唯一的办法是借助于水进行模拟分析。
相关文献对包括充填在内的，浇铸容室充填过程数字计算的使用作了论述，在此，对热力情况一起作了考虑，为找到最佳的程序设计进行了计算，了解波的传播，通过对容室内流动的研究，很有可能计算活塞运动。本文是借助于数字模拟，对浇注容室内流动力学研究，过程与选择的速度及构件第1浇注阶段的优化是重点。作为以最现代化的数字方法，对一个复杂的非线性过程研究之例，在此，优化是分成几部分自动进行，评价是以计算方法完成，所获得的认识通过实验来验证。
二、 构件几何形状及边界条件
以一个板件几何形状的生产过程为例，所作的研究示于图2.板件厚度为6mm，通过四个浇口供料。实验在埃尔兰根—纽伦堡大学金属材料与工艺实验室进行。研究工作主要集中于容室压射的过程。所用的容室长度为534mm，直径60mm，容室充填度为30%，归于较低级别。采用次级合金AlSi9Cu3，在容室内温度为680度。
 

三、 数字计算及优化
对最优化循环的控制及单个的计算是通过Surfviz软件程序进行的，该程序是由新材料FÜrth公司开发的。在浇铸容室内流动过程的个别计算是以Procast模拟平板进行的。以这样的程序可以对活塞运动说明。优化过程的流程框图及所用的程序及组成部分示于图3。计算模式可分为约770000个要素。时间分析将容室充填过程分为约600个时间步。
 

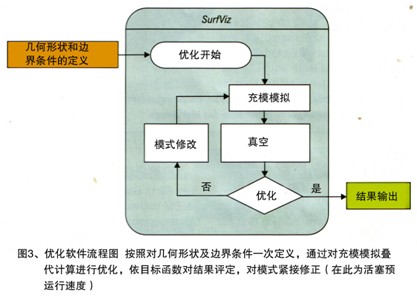
通过改变活塞预运行速度及紧接着的计值来确定优化。计算是假设第1浇铸阶段活塞速度保持常量情况下进行的。在计算中不考虑热力影响及容室充填可能的影响。流动力学过程，主要是用于研究特征类型的形成，及其评定，这是问题核心部分。
活塞速度是在优化周期循环范围内自动变化。“黄金分割”方法用作计算方法。在此所涉及的是用于近似确定目标函数极值一维的步进方法。在此确定一个研究区间，该区间内通过划分周期，识别步进极值。由于此算法不能在局部和全局极值之间进行区别，在优化过程，以逐次方法来匹配研究区间，直至找到全局最小值。将来计划使用一个优化计算方法，该方法可以在目标函数局部和全局极值之间自动识别。
目标函数是优化的基础，尤其在瞬时流动过程特性说明方面。在容室内复杂的过程，此时，是以数字来成象，此数字与优化算法的变量V1有关来应用。实质上，此说法是建立在预先开动阶段对所产生的自由表面(n)求值基础上的（图4），此时，熔化物的前沿称之为自由表面，熔化物前沿在浇铸容室内与气相接触，通常是，自由表面越少，充填过程越好。#p#分页标题#e#
 

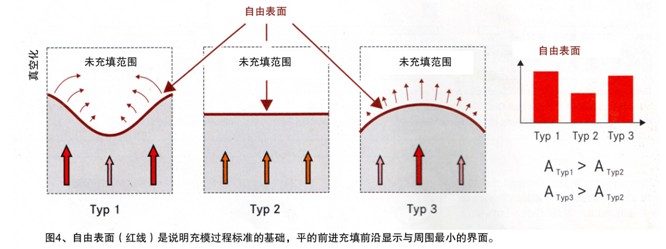
在第1阶段过程，鉴于夹杂物的形成，对自由表面计值，由此引出自由面的大小。人们认为，所产生的夹杂物为半球形的，表面积与体积之间的相关几何关系是依据。确定所有形成的各个面积，在充填过程进行研究。函数方法及算法的转化是复杂的，另作进一步论述。
四、 实验研究
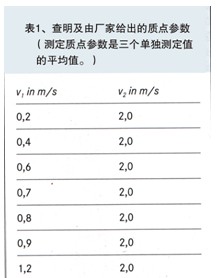
板形件的浇注是在一台闭模力为450t（约4500KN）冷室压铸机上进行的(图5)。按在表1所给预先运行速度范围为0.2-1.2，生产板件数为10，在对所属压射曲线检查之后，计值至少为5.这种方法确认，

在机器一侧所调的速度实际上也是危险的，所调的活塞预先运行速度，时常要在活塞行程30mm之后会达到。为了较好地说明所形成的孔隙度，在此不要施加增压。
模具不作强制排气，浇铸容室供料（熔化金属）是借助于一个供料机械手进行的，压射量为1250g，容室温度为160度。
 

在浇铸之后，板件从浇口分开并去毛刺，之后两个部的密度，由浮力称确定。对板件及浇口的选择研究是借助于X射线透视，依据孔隙度的形成进行的。
五、 优化结果
为了确定目标函数过程及求得全局至少42个计算，时常要以不同的 速度V1进行。单个的流动力学计算需要约2.5小时，目标函数合成曲线与工艺过程所需的时间一起示于图6，由此可以发现许多局部最

小值，主要是在很低的速度情况下，产生小的值，必须根据局部最小值，多次开始最优循环周期，在此，数值范围与变量相匹配，以便达到所述的总过程。
目标函数的过程可以分为4个特性范围（图6 Ⅰ-Ⅲ），这4个范围与浇注容室充填特殊显现相关。随后，以与活塞起始速度之关系4个速度流动情况复述（图7 、8），对其特征标记作示范性表示：在十

分低的速度下（图6范围Ⅰ），例如图7所示的0.15m/s，熔化物液面几乎是平面。金属熔化物只以很小的尺度波动，波的形成不明显，目标函数值相应小。由于活塞运行时间长（至0.2秒钟），这样低的速度缺点是在第1浇铸阶段过程，热量释放高，在第1浇铸阶段过程，热量释放高，造成提前冷凝，在此不利情况下，导致铸件局部机械性能下降，除此之外，由于温度下降，金属熔化物的粘度增加。
对于稍高的速度，如0.3m/s（图6范围Ⅱ，图8左充填序列）会形成推进波，对活塞冲击，在堵塞早期阶段，就会对浇道封堵（梗阻），而后在浇注容室出现很大的气体夹杂，压入金属熔化物内，进入物件空穴，夹杂物的形成及与之相连的自由表面的形成，会导致在图6所观察到的目标函数最大值。
过高的速度（图6Ⅲ范围，图8右边0.90m/s）会导致明显的飞弧波，由此看出空气冲入金属熔化物，目标函数值增加。在最佳情况下（v=0.73m/s），在活塞前方形成堵塞波，该波在充模过程不分离，也会导致小的飞弧波。目标函数范围Ⅲ说明形成一个稳定堵塞波。在此范围内发生预运行的波过渡至飞弧波。
因此，对于此给定的浇铸容室尺寸，在30%的容室充填度情况下，0.73m/s的活塞预运行速度是最优值，这与目标函数的最小值不相符，然而，在需要的程序时间背景下，也是最好折中。
六、 实验结果
浇口与板件在浮力称上的测定结果表示于图9.从两条曲线变化可知，在活塞预运行速度为0.7m/s时，密度为最大值，该速度值与计算求得的最优速度相当。所有V1其它实验检查值，所得密度较小。此最小值是在所用最大活塞预运行速度（1.2m/s）出现的，与预运行速度有关的密度变化，总的来说相当小。

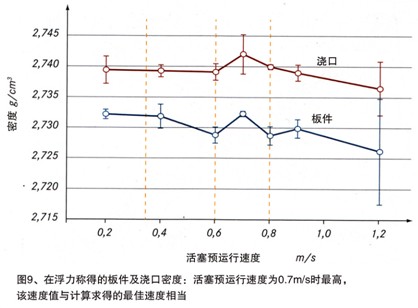
板件的密度值往往低于浇口的密度，两个部分的曲线变化相似，最高应用速度曲线变化最高。#p#分页标题#e#

图10表示透视检查的样本鉴定，所有板件均出现孔隙度，根据几何体特征（平面板件）及不规则的分布，孔隙来源于浇铸容室及空穴的充填。有些地方，速度对各孔隙的直接影响，可以当作一个变形的形式。对于0.7m/s的速度，在透视射线内的孔隙度显得最小。
七、 讨论
在考虑到运行时间情况下，计算的结果证明是一个优化的速度，该速度通过实验鉴定得以证实，尽管作了假设，在两个研究中，这样的优化证明是一致的，计算可以再现浇注容室内的过程，表现多个速度范围的特征，对于一个固定的调节值的优化与速度计算结果是相符的，该速度在活塞前可以产生一个堵塞波，此论据与文献的概括是一致的。稳定的堵塞波构成从起始运行波到飞弧波的过渡。
应用的标准，对于所研究问题具有好的适用性。各个计算的评价可以产生一个目标函数，这样的目标函数足以说明优化。
总之，构件的孔隙度是明显的，通过优化活塞预运行速度改善，使孔隙度变小是相当小，这归因于对所用模具作基本修正，这是为了生产金属泡沫开发模具。此外，在压铸构件时，不需要进行增压，所获得的结果可以看作带有方向性的，努力使所选方法对其他构件几何形状普遍适用。
八、 展望
依据所得结果，应用复杂的造型压射曲线，开始进一步研究。在此，取向于加速度，优化必须完成多个变量，应用相应算法，除此之外，可以决定局部及全局的最小值。关于对目标函数的阐述，有可能放宽围绕活塞预运行所需的运行时间直接形成夹杂的标准。